How to solve circular segments

[mklotz]

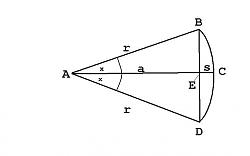
A great many machining problems mathematically involve a circular segment. The components of a circular segment are shown in the diagram below...

r = AB = AC = AD = a + s = radius of the circle
x = angle/2 = half-angle of the segment
angle = 2 * x = segment angle
BED = chord of the segment
a = AE = apothem
s = EC = saggita
arc = BCD = r * angle = circular arc of segment

If two of these elements are known, it's possible to solve for the rest. The material below shows how to do this...

NB: Note that when 'angle' is used in a computation, e.g. arc=r*angle, it must be expressed in radians, not degrees.


r & angle known:

{
a=r*cos(x)
s=r-a
chord=2.*r*sin(x)
arc=r*angle
}

r & chord known:

{
angle=2.*arcsin(0.5*chord/r)
a=r*cos(x)
s=r-a
arc=r*angle
}

r & s known:

{
a=r-s;
angle=2.*arccos(a/r);
chord=2.*r*sin(x);
arc=r*angle
}

r & arc known:

{
angle=arc/r;
a=r*cos(x);
s=r-a;
chord=2.*r*sin(x);
}

angle & chord known:

{
r=0.5*chord/sin(x);
a=r*cos(x);
s=r-a;
arc=r*angle
}

angle & s known:

{
r=s/(1.-cos(x));
a=r-s;
chord=2.*r*sin(x);
arc=r*angle
}

angle & arc known:

{
r=arc/angle;
a=r*cos(x);
s=r-a;
chord=2.*r*sin(x);
}

chord & s known:

{
r=(4.*s*s+chord*chord)/(8.*s);
a=r-s;
angle=2.*arccos(a/r);
arc=r*angle
}

The two cases (chord & arc) and (s and arc) occur very infrequently. I know of no closed solution form as above; however the program on my page will solve these cases with a convergent search algorithm.