Find circle center without a compass

[mklotz]

Many procedures for finding the center of a circle involve the use of a compass. Most shops will harbor a compass, but often it's more expedient to use only a square. Here I show how to find the center using only a square and a straightedge.



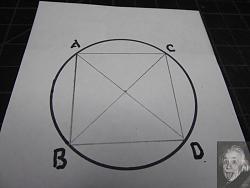
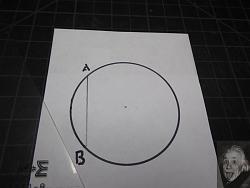
I've marked the center of the circle but only so we can see how closely the procedure finds it. The first step is to draw a chord (A-B in the photo) on one side of the circle.
The exact location, length and attitude of the chord are not critical; the only requirement is that it is not a diameter.

The next step is to use the square (I'm using a plastic drafting square) to project the A and B points onto the other side of the circle. Any "square" thing can be used, although something that lies flat, like my drafting triangle or a carpenter's square makes it easier.



This is done by aligning one side of the square with the chord and using the orthogonal side to mark the opposite side of the circle. When complete the projected points C and D define a rectangle which has the center of the circle at its center. (My "rectangle" turned out closer to a square but, trust me, the procedure works just fine if the box is more distinctly rectangular.) In practice, there's no need to draw the lines A-C, B-D, and C-D; only the A-B chord is needed. I drew the other lines for clarity only.



Now it's just a matter of drawing the diagonals of the rectangle, A-D and B-C. Where they intersect is the center of the circle.

[eimerbuilt]

Awesome! Thanks!