Calculating the radius of a circular segment

[Duke_of_URL]

There's a geometric method of solving that problem with a compass, assuming you have a 2-template of the segment:

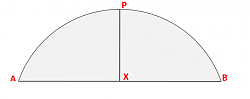
Given:



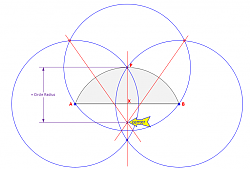
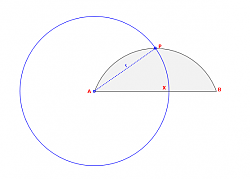
1) Using a compass create a circle at "A" using as its radius the distance AP:



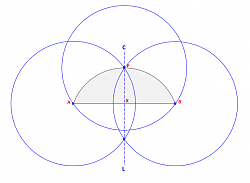
2) Now using that same radius, make corresponding circles at points B and P to locate the intersections.



3) Now using a ruler draw a line through the intersection points of each pair of circles. The intersection of those three lines will be the greater circle's center and the radius follows, as shown.

[mklotz]

Yes, that will work but using the formula will be a lot faster and requires no scaling, no template and no drafting.

[carl blum]

Hi Gang:
With no math, the two perpendicular bi-sectors of AP and PB cross at the center of the curve. A straight edge and compass job.

Here is a elliptical shaped concrete slab that is based on a gardener's ellipse done with two stakes and a bit of rope.
Carl.

[mklotz]

Hi Gang:
With no math, the two perpendicular bi-sectors of AP and PB cross at the center of the curve. A straight edge and compass job....

Yes, that will work but it requires first constructing an accurate drawing that includes the measured values for the chord and sagitta.

[carl blum]

Hi:
I'm more geometry minded: The perpendicular bisectors of AP and BP would cross the center point, as well as the bisector of AB (PQ).
Carl.

[mklotz]

Hi:
I'm more geometry minded: The perpendicular bisectors of AP and BP would cross the center point, as well as the bisector of AB (PQ).
Carl.

Yes, your technique is exactly how the center-finder attachment on a combination square works.

However, if all you have is the circular segment, then that approach requires making an accurate drawing and constructing the perpendicular bisectors, and finally measuring the radius. All those manipulations are sources for added errror and, of course, take time.


With a segment, you make two measurements and the formula provides the desired value.

A good example of this is my technique for extending the range of calipers, explained here...

Extending the range of calipers

The process directly measures the chord and sagitta and the formula introduces no additional error. (A typical scientific calculator has 12 place accuracy).

BTW, you can't get more "geometry minded" than the intersecting chords theorem. It's one of the propositions in Euclid's Elements, a 2300 year old book that was the mainstay of geometry education for many centuries.