Calculating the radius of a circular segment

[Duke_of_URL]

There's a geometric method of solving that problem with a compass, assuming you have a 2-template of the segment:

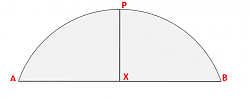
Given:



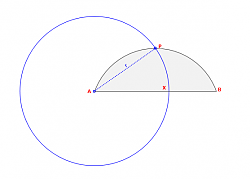
1) Using a compass create a circle at "A" using as its radius the distance AP:



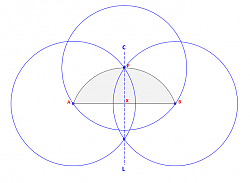
2) Now using that same radius, make corresponding circles at points B and P to locate the intersections.



3) Now using a ruler draw a line through the intersection points of each pair of circles. The intersection of those three lines will be the greater circle's center and the radius follows, as shown.

[mklotz]

Yes, that will work but using the formula will be a lot faster and requires no scaling, no template and no drafting.

[carl blum]

Hi Gang:
With no math, the two perpendicular bi-sectors of AP and PB cross at the center of the curve. A straight edge and compass job.

Here is a elliptical shaped concrete slab that is based on a gardener's ellipse done with two stakes and a bit of rope.
Carl.

[mklotz]

Hi Gang:
With no math, the two perpendicular bi-sectors of AP and PB cross at the center of the curve. A straight edge and compass job....

Yes, that will work but it requires first constructing an accurate drawing that includes the measured values for the chord and sagitta.