Calculating a circle given only an arc

[mklotz]

In geometry there is a little known theorem called the Intersecting Chords Theorem. It states that, if two chords intersect inside a circle, the product of the two sections of one chord is equal to the product of the two lengths of the other chord.

The utility of the Intersecting Chords Theorem isn't immediately obvious. This example problem demonstrates at least one use...

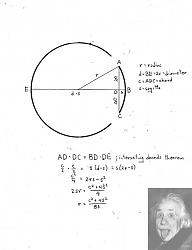
In the accompanying diagram, you're given only the partial arc of a circle ABC and must find the radius of the circle and the center on which it is drawn. The procedure for doing this is:

Draw the chord ADC.

Construct the perpendicular bisector, BDE, of the chord ADC. The diagram shows it extended to the opposite side of the circle (point E) but this point is not yet determined so, in practice, the bisector would be extended past it. No matter, the location of point E will be known once the radius is calculated and the complete circle is reconstructed. Remember that the perpendicular bisector of ANY chord passes through the center of the circle; that fact will be used later.

We now have two intersecting chords - ADC and BDE - so we can apply the Intersecting Chords Theorem. The algebra to do this is shown on the diagram. An equation for the radius is found that depends only on the lengths of the chord, ADC, and the sagitta, BD, both of which can be measured from the arc directly.

Once the radius length is calculated using the derived expression, an arc of that length swung from point A, B or C, will intersect the bisector at the center of the circle.

[meyer77]

I used that formula many years ago, when I was helping my cousin install a marble floor in a huge house.
The marble was 18"x18" about 5/8" thick.
It was set on the diagonal with a 6" border of a brown marble then finishing to the wall with the same color as the field tile.
It started at the exit of the kitchen and went down a long hall to the LR and library.
about half way down the hall there was an opening to the front entry which had two circular staircases, each had a curved face and a rounded first step, the border had to follow the radius of all three.
I did a little searching and found the formula you noted.
I ended up making a workbench that was over 8' long to which I mounted a right angle grinder vertical with diamond blade.
I had two other RA grinders set up one vertical for the out side radius and one horizontal for the inside radius.
I would hot glue a piece of wood with a pin in it to the set floor and had a piece of wood with cut to the radius with a pencil to mark the tiles.
I would then take them to the work bench and cut them to the set radius.
I would fine tune them on the two other grinders.
The largest radius was on the inside of the stairs, the next was the front of the first step, and the hardest was the small radius of end of the first step.
It took me about three weeks of cutting and fitting to finish.
At the time I did not have a digital camera and the film camera I used to take some pictures must have had a problem because it Looked like I was shooting thru a rainstorm!

[thinkbackwards]

Im sure you lost some not familiar with analytical geometry. I had to work through it once. I had not run across this theory eventhough have had many times needed it. I will add this to. notes i keep to solve problems
Thanks

[mklotz]

Im sure you lost some not familiar with analytical geometry. I had to work through it once. I had not run across this theory even though have had many times needed it. I will add this to notes i keep to solve problems
Thanks

I'm glad you found it useful.

I was surprised by the fact that no one asked for a proof of the Intersecting Chords Theorem. It's fairly easy but, if any one wants to see it, I can supply it.

[Saltfever]

Yes, Marv. Would you be so kind as to publish the proof.

All the best,
Kirk

[Saltfever]

I think Tony made a gauge based on this principal and published it here. This is an extremely useful principal when reverse engineering to get good data for an accurate CAD model.

Marv and Tony, am I on the right path here?

All the best,
Kirk

[mklotz]

Yes, Marv. Would you be so kind as to publish the proof.

All the best,
Kirk

Attached is a proof of the Intersecting Chords Theorem.

This proof makes use of some features of geometry not necessarily known to the average reader. At the risk of boring our more mathematically adept readers, I'll provide some explanations...

Two sorts of angles can be constructed in a circle. A central angle has its vertex at the center of the circle. An inscribed angle has its vertex on the circumference of a circle.

Two inscribed angles that subtend the same span on the circumference are equal.

An inscribed angle that subtends the same span as a central angle has a measure half of that of the central angle.

Both of these can be proved but, for the work here they are assumed true. (I don't want to get into an endless sequence of proofs that extend all the way back to geometric postulates/axioms (self-evident features accepted as true without proof).

Two triangles are congruent if their corresponding sides are equal in length, and their corresponding angles are equal in measure. To prove congruence you need to prove three corresponding items of the triangles are equal and at least one of those items must be a side.

Two triangles are similar if and only if corresponding angles have the same measure. If two triangles are similar, their corresponding sides will be proportional. An example might help here... All 30-60-90 triangles are similar but, in general, not congruent (unless they have an equal side). However, the ratio of the short side to the hypotenuse in all of them will be 0.5, the sine of 30 degrees.

[mklotz]

I think Tony made a gauge based on this principal and published it here. This is an extremely useful principal when reverse engineering to get good data for an accurate CAD model.

Marv and Tony, am I on the right path here?

All the best,
Kirk

Yes, you are.

Given three distinct coplanar points, it's always possible to construct a circle that passes through all three. (There are a couple of programs on my page to do this).

In my original post I used the ends of the chord and the saggital height of the arc above the midpoint of the chord. Tony's device does the same. The two outer feet determine a chord and the DI measures the saggital height above the midpoint of the chord.

There are other ways to skin this cat. The perpendicular bisector of any chord must pass through the center of the circle. Find the intersection point of the bisectors of two chords and you have the center. Once the center is known, the distance to the arc provides the radius. One of my programs uses this technique. However, it doesn't translate very well into a tool design.